The Geometric Interpretation of Cramér-Rao lower bound

I have taken the course Statistical Theory instructed by Prof.Constantine this term, focusing on the connection among decision theory, sufficient statistics, likelihood principle and evidence, and unbiased estimators and information bound.

One interesting result is his argument about Cramér-Rao lower bound. The following theorem can be found in the book: Casella and Berger, Statistical Inference.

Theorem (Cramér-Rao Inequality)

Let $X_1,…X_n$ be a sample with pdf $ f(x | \theta) $, and let $W(x)= W(X_1,...,X_n)$ be any estimator satisfying:

$\frac{d}{d \theta} E_{\theta} W(X) = \int_{X} \frac{\partial}{\partial \theta} [W(x) f(x| \theta)] dx$ and $Var_{\theta} W(x) < \infty$

Then $Var_{\theta} (W(x)) \geq \frac{(\frac{d}{d \theta} E_{\theta} W(X))^2}{E_{\theta} ((\frac{\partial}{\partial \theta} \log f(X | \theta))^2)}$

There is a geometric interpretation for CR lower bound. Consider the inner product space defined by the expected value.

For random variables $u_1$ and $u_2$, define the inner product
\[<u_1,u_2> = E(u_1 u_2)\]
Then the L2 norm of random variable $u$ is
\[\| u \| = \sqrt{E(u^2)}\]
Furthermore, if $E(u)=0 $, then $ Var(u)= E(u^2) = | u |$

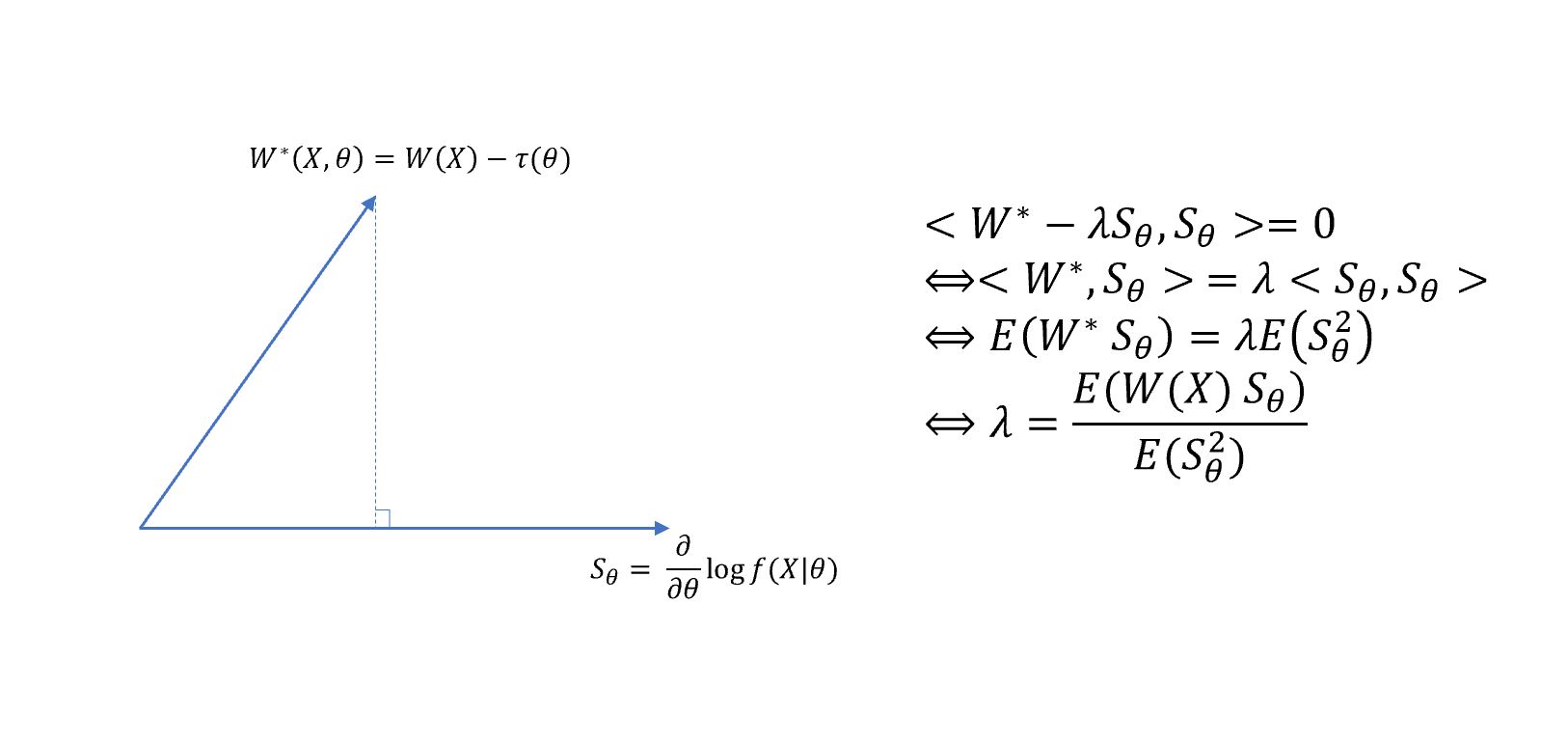
Under the regularity condition, we have the following properties:

\[\begin{align*} E(W(X) S_\theta ) &= \int W(x) \frac{\partial}{\partial \theta} \log f(x | \theta) \cdot f(x| \theta)dx \\ &= \int W(x) \frac{ \frac{\partial}{\partial \theta} f(x | \theta)} {f(x| \theta)} \cdot f(x| \theta) dx \\ &= \int W(x) \frac{\partial}{\partial \theta} f(x | \theta) dx \\ &= \frac{d}{d \theta} E_{\theta} W(x) \ \ \text{(Regularity Condition)}\\ \end{align*}\]

Let $W(X)= 1$, we will derive the expected value of the score function is 0.

\[\begin{align*} E(S_{\theta}) = \frac{d}{d \theta} 1 = 0 \end{align*}\]

Therefore,

\[\begin{align*} Var(W) & \geq Var(\lambda S_{\theta}) = \lambda^2 Var(S_{\theta}) \\ &= \frac{(\frac{d}{d \theta} E_{\theta} W(X))^2}{E_{\theta} ((\frac{\partial}{\partial \theta} \log f(X \| \theta))^2)} \\ &= \text{CRLB} \end{align*}\]

I found this geometric interpretation very helpful for understanding the attainment of CRLB, especially for multiparameter problems. The key point is to show that the best unbiased estimator lies on the plane spanned by the scores.