This post mainly focused on how to decipher the underlying mechanism of doubly robust estimators via logical operators, which was introduced in causal inference II course.
General Framework
Setup
Consider $n$ i.i.d. observations: $ \{ (X_i, Z_i, Y_i) \}_{i=1}^n$, where $X_i$ is the baseline covariates, $Z_i \in \{ 0,1 \}$ indicates the assignment of control or treatment group. $Y_i$ is the observed outcome for observation $i$.
Potential Outcome Model
Let $Y_i = Z_i Y_i(1) + (1-Z_i) Y_i(0)$, where $Y_i(z)$ is the potential outcome under treatment $z$. Therefore $Y_i(z)$ could be observed if sample $i$ is assigned to treatment $z$.
Estimand and Notations
Our goal is to estimate the average outcome if all the observations are assigned to treatment group $Z = 1$, and the subscript 0 indicates true unknown value throughout this post.
\[\tau_0 = E_0 (Y(1))\]The notations for potential outcome under treatment conditioning on covariates and propensity score are as follows :
\[\begin{align*} & y_0(x_i) = E_0 (Y_i | Z_i = 1, X_i = x_i) \\ & e_0(x_i) = Pr_0 (Z_i = 1 | X_i = x_i ) \end{align*}\]Assumptions
Assumption 1 (Strong Ignorability) \(Y_i(0), Y_i(1) \bot Z_i \ | \ X_i\)
Assumption 2 (Overlap) \(0< Pr(Z_i =1 | x_i) < 1\)
Assumption 3 (SUVTA) Stable unit treatment value assumption
Double Robustness
The following estimator is a doubly robust estimator, since it produces the correct estimation if the estimation of response surface $\hat{y}$ OR the propensity score $\hat{e}$ is correct.
\[\hat{\tau}_{DR} = \frac{1}{n} \sum \hat{y}(x_i) + \frac{y_i z_i}{\hat{e}(x_i)} - \frac{\hat{y}(x_i) z_i}{\hat{e}(x_i)}\]Logical Operators Characterization
We define the AND operator as
\[\tau^{AND}(y,e) = \tau_0 \ \text{if} \ y=y_0 \ \text{AND} \ e = e_0\]we then introduce OR operator as
\[\tau^{OR}(y,e) = \tau^{AND}(y,e_0) + \tau^{AND}(y_0,e) - \tau^{AND}(y,e)\]We could observe that AND operator gives correct estimation if both $y$ and $e$ are correct, while OR operator gives correct estimation if at least one of $y$ and $e$ is correct.
Next, we intuitively demonstrate that the above doubly robust estimator belongs to OR operator class.
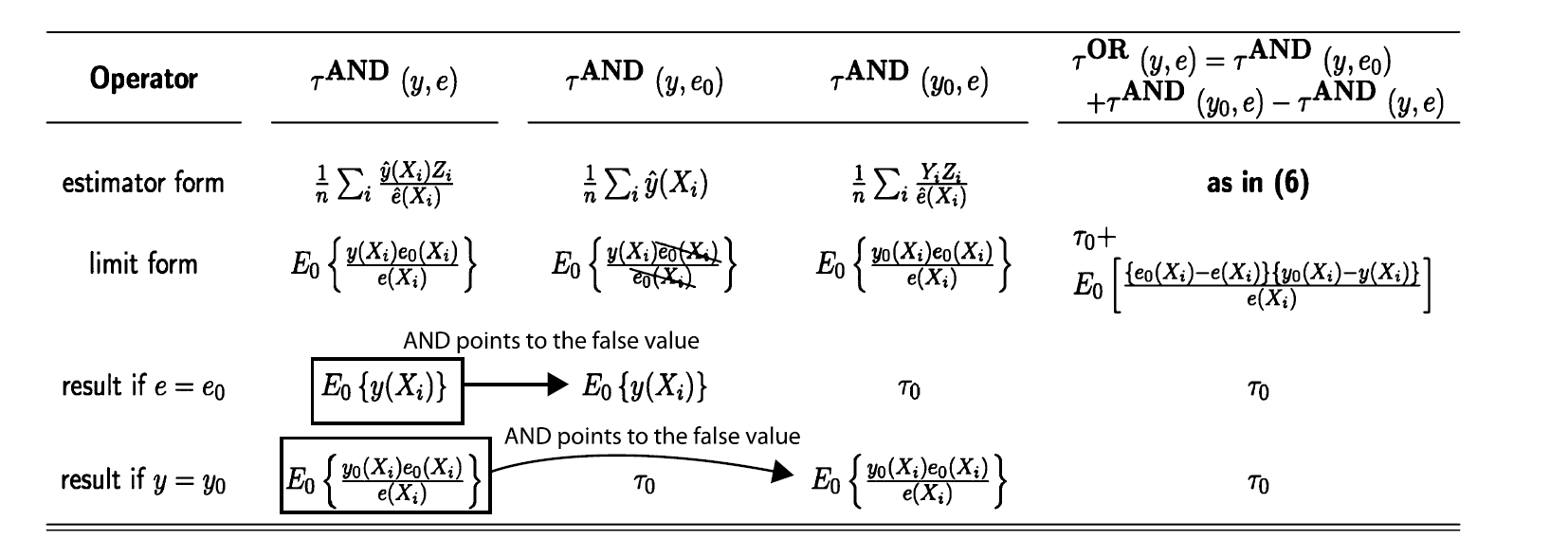
From the above figure, we could reformulate the doubly robust estimator as
\[\hat{\tau}_{DR} = \frac{1}{n} \sum \underbrace{\hat{y}(x_i)}_{\tau^{AND}(y,e_0)} + \underbrace{\frac{y_i z_i}{\hat{e}(x_i)}}_{\tau^{AND}(y_0,e)} - \underbrace{ \frac{\hat{y}(x_i) z_i}{\hat{e}(x_i)}}_{\tau^{AND}(y,e)}\]The double robustness property of OR operators could be illustrated in the following scenarios:
-
$ \hat{e} = e_0$ and $\hat{y} = y_0$ (both the propensity score model and response surface model are correct)
All the three AND estimators $\to$ true value $\tau_0$. -
$ \hat{e} = e_0$ but $\hat{y} \neq y_0$ (the propensity score model is correct while the response surface model is incorrect)
\(\tau^{AND}(y_0,e) \to \tau_0\); \(\tau^{AND}(y,e) \ \text{and} \ \tau^{AND}(y,e_0) \to\) same incorrect value. Therefore, the OR operator could offset the incorrect value. -
$ \hat{y} = y_0$ but $\hat{e} \neq e_0$ (the response surface model is correct while the propensity score model is incorrect)
\(\tau^{AND}(y,e_0) \to \tau_0\); \(\tau^{AND}(y,e) \ \text{and} \ \tau^{AND}(y_0,e) \to\) same incorrect value. Therefore, the OR operator could offset the incorrect value.
Reference
[1] Frangakis, C. (2019). A Falsifiability Characterization of Double Robustness Through Logical Operators. Journal of Causal Inference, 7(1).
[2] Lecture notes from the course: Causal Inference II , instructor: Prof.Constantine Frangakis and Prof. Betsy Ogburn